UbiquitousAngles

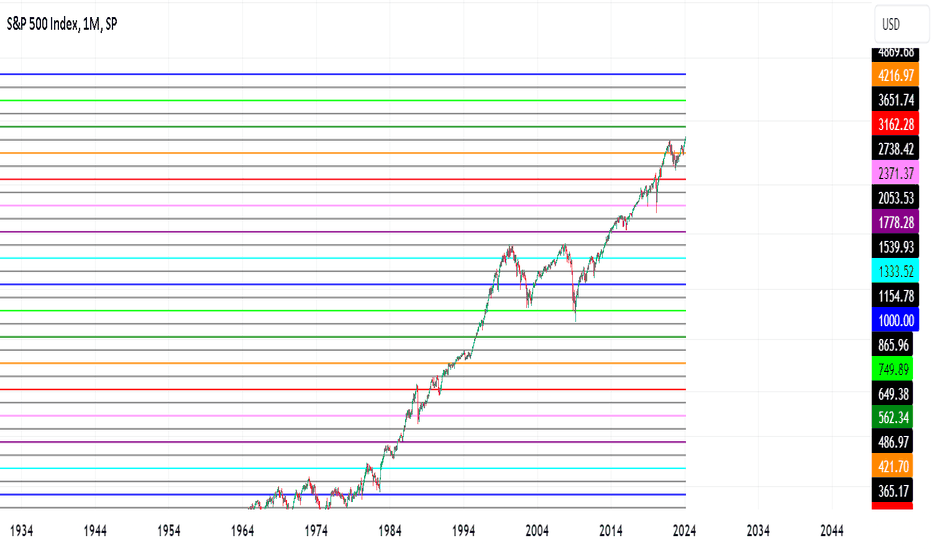
همانطور که در پست های قبلی برای سایر دارایی ها نشان داده ام ، این سطح قیمت مورد انتظار است که به عنوان نقاط میانی پیروی از قانون بنفورد ، که به عنوان قانون اعداد غیر عادی نیز شناخته می شود ، توضیح داده شده است. حتی اگر این شبکه های نشان داده شده همیشه سطح قیمت معکوس نیستند ، ما می بینیم که اغلب اوقات این نقاط میانی در واقع act به عنوان پشتیبانی یا مقاومت انجام می شود ، و نقاط میانی بین نقاط میانی نشان داده نشده است که نشان داده شده است act به عنوان سطح قیمت مربوطه. احتمال ارقام پیشرو طبق قانون بنفورد: P (1) = 30.1 ٪ P (2) = 17.6 ٪ P (3) = 12.5 ٪ P (4) = 9.7 ٪ P (5) = 7.9 ٪ P (6) = 6.7 ٪ P (7) = 5.8 ٪ P (8) = 5.1 ٪ P (9) = 4.6 ٪ افسانه: 1.33 آبی روشن 1.78 بنفش 2.37 صورتی 3.16 red 4.21 نارنجی 5.62 سبز تیره 7.50 سبز روشن 10 آبی تیره سفارش بعدی نقاط میانی به رنگ خاکستری برای توضیح کامل تر در مورد این روش ، پیوندهای زیر را بررسی کنید.

طلا دارایی دیگری است که من از آن پیروی می کنم و تعجب نمی کنم که آن را به اصل میانه ها که توسط قانون بنفورد توضیح داده شده است ، که به عنوان قانون اعداد غیر عادی نیز شناخته شده است ، تعجب نمی کنم. این شبکه هایی که من ترسیم کرده ام ، نقاط میانی هستند و در یک نمودار لگاریتمی مشاهده می شوند تا بتوانیم آسانتر نرخ تغییر را در بزرگی قیمت در مدت زمان طولانی مقایسه کنیم. من دلیل منطقی را در پست های قبلی توضیح داده ام ، که می توانید در لینک های زیر مشاهده کنید. احتمال ارقام پیشرو طبق قانون بنفورد: P (1) = 30.1 ٪ P (2) = 17.6 ٪ P (3) = 12.5 ٪ P (4) = 9.7 ٪ P (5) = 7.9 ٪ P (6) = 6.7 ٪ P (7) = 5.8 ٪ P (8) = 5.1 ٪ P (9) = 4.6 ٪ افسانه: 1.33 آبی روشن 1.78 بنفش 2.37 صورتی 3.16 red 4.21 نارنجی 5.62 سبز تیره 7.50 سبز روشن 10 آبی تیره سفارش بعدی نقاط میانی به رنگ خاکستری

من قبلاً قانون اعداد غیر عادی را که به عنوان قانون بنفورد نیز شناخته می شود ، معرفی کرده ام. در حالی که استفاده از مقیاس قیمت لگاریتمی به تغییر قیمت در طول زمان کمک می کند ، من خطوط اضافی را به همان اندازه در هر بزرگی قرار داده ام تا بیشتر عملکرد قیمت را روشن کنم. من ابتدا با گرفتن ریشه مربع 10 ، که برابر با 3.16 است ، هر بزرگی را به نصف تقسیم کردم. قانون بنفورد در بازارهای مالی اعمال می شود ، نشان می دهد که قیمت باید نیمی از زمان را بین 1*10^x و 3.16*10^x و نیمی دیگر از زمان بین 3.16*10^x و 1*10^(x+1) بگذراند ، و غیره. با وجود این نمایندگی ، ما فقط به رقم پیشرو نگران هستیم ، بنابراین قیمت لازم نیست هر زمان مساوی را در هر زمان بگذرانیم. هرچه مدت زمان و سفارشات بزرگی در قیمت ما اندازه گیری شود ، احتمال رقم پیشرو به سمت توزیع قانون قدرت که در زیر مشاهده می شود ، بیشتر می شود. باید توجه داشته باشیم که به نظر می رسد که ارقام بعدی از این توزیع نیز پیروی می کنند اما به سمت توزیع یکنواخت حرکت می کنند و دورتر از رقم پیشرو اندازه گیری می کنیم. این مستقل از سیستم شماره پایه مورد استفاده است و با استفاده از دیدگاه درصد تغییر ، به راحتی قابل درک است. احتمال ارقام پیشرو: P (1) = 30.1 ٪ P (2) = 17.6 ٪ P (3) = 12.5 ٪ P (4) = 9.7 ٪ P (5) = 7.9 ٪ P (6) = 6.7 ٪ P (7) = 5.8 ٪ P (8) = 5.1 ٪ P (9) = 4.6 ٪ افسانه و نحوه کسب هر شماره اما به ترتیب عددی ترتیب داده می شود: SQRT (1.78) = 1.33 آبی روشن SQRT (3.16) = 1.78 بنفش 1.33*1.78 = 2.37 صورتی SQRT (10) = 3.16 red 1.33*3.16 = 4.21 نارنجی 1.78*3.16 = 5.62 سبز تیره 2.37*3.16 = 7.50 سبز روشن 10 آبی تیره سفارش بعدی نقاط میانی به رنگ خاکستری به نظر من جالب است که چگونه میانه نقاط میانی نقاط میانی و غیره ، به نظر می رسد که به طور مداوم با قیمت به عنوان پشتیبانی و مقاومت در تعامل هستند و نه اینکه فقط یک شماره دلخواه در طول یک پیاده روی تصادفی باشد. اگر ما همچنان به نقاط میانی نقاط میانی بی نهایت برداریم ، به طور طبیعی هر شماره را پر کرد. سپس ما جمع می کنیم که مهمترین تعداد 1 (در میان بزرگی) و به دنبال آن نقطه میانی آن (3.16) و به دنبال آن نقاط میانی نقطه میانی (1.78 و 5.62) ، و به دنبال آن نقاط میانی نقاط میانی (1.33 ، 2.37 ، 4.21 و 7.5) و غیره است. این سطح قیمت علت نیست ، اما همانطور که در این نمودار و سایرین مشاهده می شود ، با این اثر به هم پیوسته است.

برای بسیاری از عوامل بازی حتی به زمان بندی تغییر پارادایم نزدیک می شود ، اما با ادامه زمان ارائه شواهد پشتیبانی ، این پایان نامه بدون تغییر باقی مانده است. ارزهای فیات بر بدهی ساخته شده اند که یک عنصر زمان دارد. از آنجایی که زمان ثابت است و نمی توان دستکاری کرد ، تمام کاری که باید انجام دهیم به عنوان سرمایه گذاران منتظر هستند. پول بیشتری در دراز مدت به عنوان یک محصول جانبی از بانکها که با ذخایر کسری کار می کنند و به دلیل اقدامات خارق العاده ای که توسط فدرال رزرو به سمت پایان چرخه های اعتباری انجام می شود ، به منظور نرم شدن تصادف اجتناب ناپذیر و تحریک رونق بعدی ادامه یافت. هیچ تحمل برای تورم طولانی مدت وجود ندارد زیرا سالها تورم متوسط به طور معمول انتظار می رود ، و حلقه بازخورد مثبت در طول شلوغی که از آنجا که بدهی نمی تواند بازپرداخت شود ، فوری و شدیدتر است. این پیش بینی با استفاده از "الگوی میله ها" ایجاد شده است

زاویه های متعدد در بازه های زمانی که در حال حاضر همگرا هستند ، بنابراین قیمت bitcoin safe در حال حاضر در اینجا در وسط است. شرط بندی های سنگین در هر دو جهت قرار دارند. نوسانات تا پایان ماه پیش بینی می شود (چه زمانی اینطور نیست؟) ؛ +/- 33 ٪ یا 24K $ - 48K $.